BAB 2 ( BAHAGIAN 4) PART2

The limits of Bernoulli’s Equation
Bernoulli’s Eqution is the most important and useful equation in fluid mechanics. It may be written,

 Bernoulli’s Equation has some restrictions in its applicability
: ƒ the flow is steady
 ƒ the density is constant (which also means the fluid is compressible)
ƒ friction losses are negligible
ƒ the equation relates the state at two points along a single streamline (not conditions on two different streamlines).
Application of Bernoulli’s Equation
Bernoulli’s equation can be applied to the following situations.

Pressure/velocity variation

Consider the steady, flow of a constant density fluid in a converging duct, without losses due to friction (figure 14). The flow therefore satisfies all the restrictions governing the use of Bernoulli's equation. Upstream and downstream of the contraction we make the one-dimensional assumption that the velocity is constant over the inlet and outlet areas and parallel.

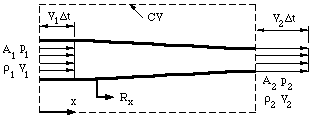Figure   .One-dimensional duct showing control volume. MUHAMMAD FAIZAL BIN AZAMI 13DEM18F1073